What can a mathematician tell you about plants
When you picture a biologist, who do you have in your mind? When you picture a biology lab, what do you see? A bench, a flask, a shaker, maybe huge centrifuge? White coat, numerous Petri dishes, floating smell of bacteria and some disposable gloves? Well, it is definitely how I pictured it before I became a biologist myself. A biologist that actually quite often is being refused to call herself that way, as on a daily basis I am not using any of the things mentioned above, just a computer do the work. So you should start to wonder, what on earth can a mathematician tell you about plants.
Few words on photosynthesis
You probably know something about photosynthesis. Through a series of reactions plants are capable of converting energy harvested from light into chemical one, that fuels their metabolism and constitute source of life on Earth. Right? But did you ever hear about state transitions or nonphotochemical quenching? Did you know that plants developed various sophisticated mechanisms that allow them to maintain photosynthetic efficiency despite constantly changing environmental conditions? When plants are lacking solar energy they try to absorb as much of given light as possible, on the other hand when the radiance is too strong, they ‘waste’ energy through heat dissipation to protect themselves against damage. The way photosynthetic organisms are tuned to capture solar energy amazes researchers.
If we could only understand better the processes that are involved in capturing and transferring light energy. Clearly, a precise understanding of what is guiding plants responses is required to optimize biotechnological exploitation of photosynthetic organisms, for example, for the production of high-value commodities, such as cosmetics or pharmaceuticals. Such an understanding, which can only be obtained by combining several scientific approaches, will allow to assess, quantify and eventually minimize the rate of energy loss and my method of choice to study those intrinsic mechanisms is through mathematical modelling.
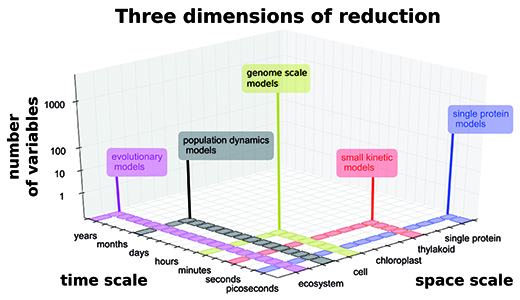
Model as a simplification of reality
Properly constructed mathematical models are a powerful tool to discover organizational principles governing the design of biological systems. They can take many forms, depending on the research question they aim to answer but they will always constitute a simplified version of reality (see Figure 1). They can reduce the complexity focusing only on processes that are happening very fast (within seconds, like charge separation) or the one that takes whole decades to occur (like in the case of evolution). They can focus on a single process or a whole network. It is a true challenge to reduce the model to the minimal set of reactions within which you can reproduce and study your system. That is why the model I am developing resembles with its structure a construction build from Lego bricks, that depending on the questions I wish to answer I can reduce and expand my space.
Building models like playing with Lego
Based on our current understanding of the photosynthesis, we can divide reactions into two major sets: the one that starts with the absorption of light and ends up with the synthesis of ATP (often refereed to as light reactions) and the second one during which the energy from ATP and reducing powers is utilized to produce sugars through carbon fixation cycle.
Therefore to start building a detailed model where we want to follow how changes in the light affect photosynthetic efficiency in terms of biomass production, we start small, focusing on how light is absorbed and simply converted to ATP and NADPH. We reduce the timescale to processes occurring within seconds to minutes, the space scale to the reactions taking place inside of the thylakoid membrane (inside of the chloroplast) and the number of unknown to follow to six (core model published by my Ebenhöh et al. 2014). This simple model will already give us some understanding on how the system works but will not bring any insight into photoprotective mechanisms, as there are non implemented. Therefore we can construct a small additional script that will include mechanisms responsible for optimal energy distribution (called state transitions, but only for those really interested in the topic) and increase our parameters space (we need to know how fast certain processes occur) and number of variables. In a similar manner we can keep adding small building blocks, adding more detailed processes or removing nonexistent, finally merging the light reactions with the carbon fixation.
Once ‘the tower’ is up, you are free to play with different combinations: impact of the excess of light on the plant that doesn’t have the genes responsible for energy dissipation: remove the red block. Study how plant will change the production of sugars if we increase it’s capability of optimal energy distribution: change parameters within the green block. Study the same processes in plants that are more efficient in carbon fixation: change the dark green block with another script.
My work is supported by the Marie Curie Initial Training Network AccliPhot funded by the European Commission under the Seventh Framework Programme (SP3-People) under the grant agreement number PITN-GA-2012-316427
Contribution by Anna Matuszyńska, Institute for Quantitative and Theoretical Biology, HHU
Planter’s Punch
Under the heading Planter’s Punch we present each month one special aspect of the CEPLAS research programme. All contributions are prepared by our young researchers.
Corresponding publications
A. Matuszyńska, O. Ebenhöh, A reductionist approach to model photosynthetic self-regulation in eukaryotes in response to light. Biochemical Society transactions 43, 1133-1139 (2015); published online EpubDec 1 (10.1042/BST20150136). [Abstract]
Ebenhöh O, Fucile G, Finazzi G, Rochaix JD, Goldschmidt-Clermont M (2014) Short-term acclimation of the photosynthetic electron transfer chain to changing light: a mathematical model. Philosophical transactions of the Royal Society of London. Series B, Biological sciences 369(1640):20130223. [Abstract]